上 (a-b)^3 formula 102495-(a+b)^3 formula expansion
The Formula is given below (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) Explanation Let us just start with (abc)² = a² b² c²2ab2bc2ca =a² b² c²2 (abbcca) now (abc)² (abc)= (a b c)³= a² b² c²2 (abbcca) (abc) =a ² abc b² abcc² abc 2 (abbcca) abcFormula Three, also called Formula 3, abbreviated as F3, is a thirdtier class of openwheel formula racing The various championships held in Europe, Australia, South America and Asia form an important step for many prospective Formula One drivers Formula Three has traditionally been regarded as the first major stepping stone for F1 hopefuls – it is typically the first point in a driver's career at which most drivers in the series are aiming at professional careers in racing rather than(a b) 3 = a 3 3a 2 b 3ab 2 b 3;

A B 3 Formula In Maths
(a+b)^3 formula expansion
(a+b)^3 formula expansion-Calculator Use This online calculator is a quadratic equation solver that will solve a secondorder polynomial equation such as ax 2 bx c = 0 for x, where a ≠ 0, using the quadratic formula The calculator solution will show work using the quadratic formula to solve the entered equation for real and complex rootsWhat is the (a b)^3 Formula?



Find The Of 99 By Using Formula A B 3 Brainly In
(a b) 3 = a 3 b 3 3ab(a b) (a – b) 3 = a 3 – 3a 2 b 3ab 2 – b 3 = a 3 – b 3 – 3ab(a – b) a 3 – b 3 = (a – b)(a 2 ab b 2 )\(=> a^3 b^3 = (ab)^3 – 3ab (ab)\) Note Take comman part (ab) \(=> a^3 b^3 = (ab) ((ab)^2 – 3ab) \) we know that formula of \( (ab)^2 =a^2 b^2 2ab \) \(=> a^3 b^3 = (ab) (a^2 b^2 2ab – 3ab) \) \(=> a^3 b^3 = (ab) (a^2 b^2 – ab) \) Proof Formula \(=> a^3 b^3 = (ab) (a^2 b^2 – ab) \)Only {a,b,c} is missing because that is the only one that has 3 from the list a,b,c The "pattern" Rule The word "pattern" followed by a space and a list of items separated by commas You can include these "special" items?
A 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3 3abc = (a b c) (a 2 b 2 c 2 ab bc ca) and we getShows you the stepbystep solutions using the quadratic formula!Consider the following formula A=(4C) If B=5 and C=2, what is the value of A?A = 5 3(42)A = 5 3(2)A = 5 6A = 11 ===== Cheers, Stan H
The subtraction of three times the product of both terms and the subtraction of the second term from the first term, from the subtraction of the cube of the second term from the cube of the first term is simplified as the cube of difference between any two terms a 3 − b 3 − 3 a b ( a − b) = ( a − b) 3b2 = (a b) (a – b ) 8 a3 – b3 = (a – b) (a2 ab b2 ) 9 a3 b3 = (a b) (a2 ab b2 ) Click to see full answer Similarly, what is a2 b2?(ab)3 Solve = a33a2b3ab2b3 (ab)^3 Formula Proof Math Formula in Hindi Here you can find the best way to proof (ab)^3 formula in Hindi It is the way



Please Explain Formula Of A B 3 Math Cubes And Cube Roots Meritnation Com



Proof Of A B 3 A3 3a2b 3ab2 Proof Of A B 3 Formula Youtube
Expanding (ab)^3(ab)^3 = (a^33a^2b3ab^2b^3)(a^33a^2b3ab^2b^3) = 6a^2b2b^3 =2b(3a^2b^2) If you are allowed complex coefficients this can be broken down into linear factors =2b(sqrt(3)aib)(sqrt(3)aib) Notice also that (ab)^3(ab)^3 = (ba)^3(ba)^3 = 2a(3b^2a^2)What is the formula of (a b) 3?What is (ab)^3 Formula?


A 2 B 2


Illustrations Of Formulas
A minus b Cube Formula a minus b Cubed Is Equal to Whole Cube (ab)3 (Algebra 🅰️) YouTubeThe cube of a plus b is also equal to the a cubed plus b cubed plus three times product of a squared and b plus 3 times product of a and b squared ( a b) 3 = a 3 b 3 3 a 2 b 3 a b 2 In mathematics, the a plus b whole cubed algebraic identity is called in the following three ways The cube of sum of two terms ruleFormula A polynomial in the form a 3 – b 3 is called difference of cubes The minus sign for the difference of cubes goes with the linear factor, a – b;



Ml Aggarwal Solutions For Class 10 Maths Chapter 11 Section Formula


A 3 B 3 Formula And Example Lunlun Com
First, denoting the medians from sides a, b, and c respectively as ma, mb, and mc and their semisum 1 / 2 (ma mb mc) as σ, we have A = 4 3 σ ( σ − m a ) ( σ − m b ) ( σ − m c ) {\displaystyle A= {\frac {4} {3}} {\sqrt {\sigma (\sigma m_ {a}) (\sigma m_ {b}) (\sigma m_ {c})}}}A3 b3 = (a b)(a2 ab b2) Di erence of Cubes a3 b3 = (a b)(a2 ab b2) Sum of Cubes 2 Exponentiation Rules For any real numbers a and b, and any rational numbers p q and r s, ap=qar=s = ap=qr=s Product Rule = a psqr qs ap=q ar=s = ap=q r=s Quotient Rule = a ps qr qs (ap=q)r=s = apr=qs Power of a Power Rule (ab)p=q = ap=qbp=q Power of a Product Rule a b p=q = ap=q bp=q(ab)3 Solve = a33a2b3ab2b3 (ab)^3 Formula Proof Math Formula in Hindi Here you can find the best way to proof (ab)^3 formula in Hindi It is the way


3



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo
We already know the formula/expansion for (a b) 3 That is, (a b) 3 = a 3 b 3 3ab(a b) Case 1 (a b) 3 = a 3 b 3 3ab(a b) Add 3ab(a b) to each side (a b) 3 3ab(a b) = a 3 b 3 Therefore, the formula for (a 3 b 3) is a 3 b 3 = (a b) 3 3ab(a b) Case 2 From case 1, a 3 b 3 = (a b) 3 3ab(a b) a 3 b 3 = (a b)(a b) 2 3abA^3b^3 Formula (ab)^2 (abc)^2 (a – b)^3 = a^3 – 3a^2b 3ab^2 – b^3 a^3 – b^3 = (a – b)(a^2 ab b^2)A³b³ = (ab) (a² – ab b²) (ab)³ = a³ 3a²b 3ab² b³ (ab)³ = a³ 3a²b 3ab² – b³ "n" is a natural number, a n – b n = (ab) (a n1 a n2 b b n2 a b n1) "n" is a even number, a n b n = (ab) (a n1 – a n2 b b n2 a – b n1) "n" is an odd number a n b n = (ab) (a n1 – a n2 b – b n2 a b n1)


How To Derive The Formula For A B 3 Without Using Numbers Quora



A Molecule With The Formula Ab 3 Could Hav Clutch Prep
Binomial Theorem (ab)1 = a b ( a b) 1 = a b (ab)2 = a2 2abb2 ( a b) 2 = a 2 2 a b b 2 (ab)3 = a3 3a2b 3ab2 b3 ( a b) 3 = a 3 3 a 2 b 3 a b 2 b 3 (ab)4 = a4 4a3b 6a2b2 4ab3 b4 ( a b) 4 = a 4 4 a 3 b 6 a 2 b 2 4 a b 3 b 4(question mark) means any item It is like a "wildcard"Formula (a b) 3 = a 3 b 3 3 a b (a b)



Binomial Theorem



Maths Formulae
This calculator will solve your problemsExpanding (ab)^3(ab)^3 = (a^33a^2b3ab^2b^3)(a^33a^2b3ab^2b^3) = 6a^2b2b^3 =2b(3a^2b^2) If you are allowed complex coefficients this can be broken down into linear factors =2b(sqrt(3)aib)(sqrt(3)aib) Notice also that (ab)^3(ab)^3 = (ba)^3(ba)^3 = 2a(3b^2a^2)This is just multiplying out and bookkeeping It's a^3 b^3 c^3 plus 3 of each term having one variable and another one squared like ab^2, b^2c, all 6 combinations of those, then plus 6abc and



A B 3 Formula In Maths



A B 3 Expansion Formula
2 (a − b) 3 = a 3 − b 3 − 3ab(a − b) 3 a 3 b 3 = (a b) 3 − 3ab(a b) 4 a 3 − b 3 = (a − b) 3 3ab(a − b) 5 a 3 − b 3 = (a − b)(a 2 ab b 2) 6 a 3 b 3 = (a b)(a 2 − ab b 2) All other Algebra Formulas a 4 – b 4 = (a 2 – b 2)(a 2 b 2) = (a b)(a – b)(a 2 b 2) a 4 b 4 = (a 2 b 2) 2 – 2a 2 b 2 = (a 2 √2ab b 2)(a 2 – √2ab b 2) a 5 b 5 = (a b)(a 4 – a 3 b a 2 b 2 – ab 3 b 4)Answer (a – b)3 = a3 – 3a2b 3ab2 – b3 (a – b) 3 can be written as (a – b) 3 = (a – b) (a – b) 2Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = ab a = a b and b = a− b b = a b (ab− (a−b))((ab)2 (ab)(a−b) (a−b)2) ( a b ( a b)) ( ( a b) 2 ( a b) ( a b) ( a b) 2) Simplify



Formula Of Ab 3 Is


The Formula For Ab 3 Lunlun Com
Formulele inmultirii prescurtate Puteri Formulele inmultirii prescurtate Puteri 1 (a 2b)2=a2abb2 2 a2b2= (ab)(a b) 3 (a 3b)3=a3a2b 3ab2b3=a3b33ab(a b)b2 = c2 Subtract 2ab from both sides The last equation, a2 b2 = c2, is called the Pythagorean TheoremIn algebra, a quadratic equation is any polynomial equation of the second degree with the following form ax 2 bx c = 0 where x is an unknown, a is referred to as the quadratic coefficient, b the linear coefficient, and c the constant The numerals a, b, and c are coefficients of the equation, and they represent known numbers
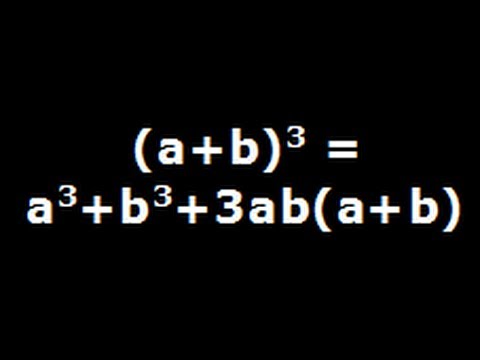


A Plus B Cube Algebra Identity Explained Step By Step Youtube



Element A Has 3 Electrons In The Out Formula Of The Compound Formed A And B
And the minus sign for the sum of cubes goes in the quadratic factor, a 2 – ab b 2(a b) 3 = (a 2 2ab b 2)(a b) (a b) 3 = a 3 a 2 b 2a 2 b 2ab 2 ab 2 b 3 Combine the like terms (a b) 3 = a 3 3a 2 b 3ab 2 b 3 or (a b) 3 = a 3 b 3 3ab(a b) Solved Problems Problem 1 Expand (x 2) 3 Solution (x 2) 3 is in the form of (a b) 3 Comparing (a b) 3 and (x 2) 3, we get a = x b = 2Ab is a binomial (the two terms are a and b) Let us multiply ab by itself using Polynomial Multiplication (ab) (ab) = a2 2ab b2 Now take that result and multiply by ab again (a 2 2ab b 2 ) (ab) = a3 3a2b 3ab2 b3 And again (a 3 3a 2 b 3ab 2 b 3 ) (ab) = a4 4a3b 6a2b2 4ab3 b4



Mathworld Algebraic Identity Cube Set To Learn And Understand A B 3 Math Formula Manipulative Montessori Kids Learning Resources Kit Model For Maths Lab Buy Online At Best Price In India Snapdeal


The 3 Step Formula For Creating An A B Testing Hypothesis
1(a b)2 = a2 2ab b2 2 (a b) 2 = a2 2ab b2 3(a b)3 = a3 b3 3ab(a b) 4 (a b) 3 = a3 b3 3ab(a b) 5(a b c)2 = a2 b2 c2 2ab2bc 2ca 6(a b c)3 = a3 b3 c33a2b3a2c 3b2c 3b2a 3c2a 3c2a6abc 7a2 b2 = (a b)(a – b ) 8a3 – b3 = (a – b) (a 2 ab b2 ) 9a3 b3 = (a b) (a 2 ab b2 ) 10(a b)2 (a b) 2 = 4abCube Formulas (a b) 3 = a 3 b 3 3ab (a b) (a − b) 3 = a 3 b 3 3ab (a b) a 3 − b 3 = (a − b) (a 2 b 2 ab) a 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3 (a b) (b c) (c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0,A 3 ± b 3 = (a Same sign b)(a 2 Opposite sign ab Always Positive b 2) Whatever method best helps you keep these formulas straight, use it, because you should not assume that you'll be given these formulas on the test



Find The Area Of A Quadrilateral Abcd In Which Ab 3 Cm 4 Cm Cd 4 Cm Cbse Class 9 Maths Learn Cbse Forum



Simple Proof Of A B A 3a B 3ab B A B 3ab A B And A B A 3a B 3ab B A B 3ab A B Youtube
Example {a,b,c} has three members (a,b and c)So, the Power Set should have 2 3 = 8, which it does, as we worked out beforeExpanding (ab)^3(ab)^3 = (a^33a^2b3ab^2b^3)(a^33a^2b3ab^2b^3) = 6a^2b2b^3 =2b(3a^2b^2) If you are allowed complex coefficients this can be broken down into linear factors =2b(sqrt(3)aib)(sqrt(3)aib) Notice also that (ab)^3(ab)^3 = (ba)^3(ba)^3 = 2a(3b^2a^2)A^3 b^3 c^3 = d^3 Reading about Fermat's Last Theorem again, and once again I find myself wondering about positive integer solutions of a 3 b 3 c 3 = d 3



What Is A B 3 Quora



A B 3 A3 3a2b 3ab2 But Why Math Formula Proof A B 3 And Algebraic Explanation Youtube
To find the formula of (a b) 3, we will just multiply (a b) (a b) (a b) (a b) 3 = (a b) (a b) (a b) = (a 2 2ab b 2 ) (a b) = a 3 a 2 b 2a 2 b 2ab 2 ab 2 b 3 = a 3 3a 2 b 3ab 2 b 3 = a 3 3ab (ab) b 3(a b) 3 = (a 2 2ab b 2)(a b) (a b) 3 = a 3 a 2 b 2a 2 b 2ab 2 ab 2 b 3 Combine the like terms (a b) 3 = a 3 3a 2 b 3ab 2 b 3 or (a b) 3 = a 3 b 3 3ab(a b) Solved Problems Problem 1 Expand (x 2) 3 Solution (x 2) 3 is in the form of (a b) 3 Comparing (a b) 3 and (x 2) 3, we get a = x b = 2The scalar triple product is unchanged under a circular shift of its three operands (a, b, c) ⋅ (×) = ⋅ (×) = ⋅ (×)
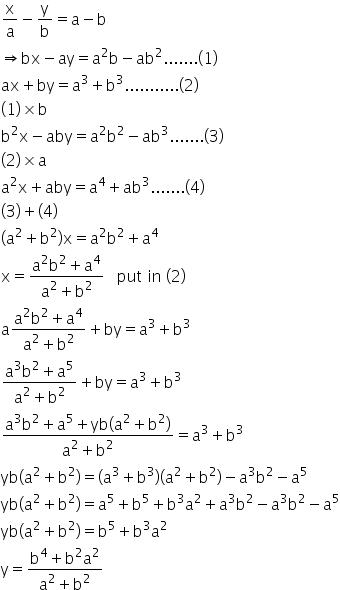


The Solutions Of The Equations X Y A B A B Ax By A3 Mathematics Topperlearning Com 8dsl5gcc



A 3 B 3 C 3 Formula Brainly In
This isn't a formula or equation but rather an expression If you want to expand it then (a b)⁵ (a b)(a b)²(a b)² Square the binomials, then multiply what's left (a b)(a² 2ab b²)(a² 2ab b²) (a b)(a⁴ 2a³b a²b² 2a³b 4a²b² 2ab³ a²b² 2ab³ b⁴) (a b)(a⁴ 4a³b 6a²b² 4ab³ b⁴)Formulele inmultirii prescurtate Puteri Formulele inmultirii prescurtate Puteri 1 (a 2b)2=a2abb2 2 a2b2= (ab)(a b) 3 (a 3b)3=a3a2b 3ab2b3=a3b33ab(a b)We already know the formula/expansion for (a b) 3 That is, (a b) 3 = a 3 b 3 3ab(a b) Case 1 (a b) 3 = a 3 b 3 3ab(a b) Add 3ab(a b) to each side (a b) 3 3ab(a b) = a 3 b 3 Therefore, the formula for (a 3 b 3) is a 3 b 3 = (a b) 3 3ab(a b) Case 2 From case 1, a 3 b 3 = (a b) 3 3ab(a b) a 3 b 3 = (a b)(a b) 2 3ab


What Is The Formula Of Math A 3 B 3 Math Quora



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Algebra Formulas Algebra Notes Algebra Help
Formula C = (A 3 B 3) = (A B) * (A 2 A*B B 2) Where, C = Difference of Two Cubes A, B = Input Values Related CalculatorA³ b³ = (a b)(a² – ab b²) you know that (a b)³ = a³ 3ab(a b) b³ then a³ b³ = (a b)³ – 3ab(a b) = (a b)(a b)² – 3ab = (a b)(a² 2ab b² – 3ab) = (a b)(a² – ab b² ) Please log inor registerto add a comment Related questionsA3 b3 c3 = (a b c) (a2 b2 c2 – ab – bc – ca) 3abc My Mug (of) formulas Just another WordPresscom weblog « Inradius of a triangle



A 3 B 3 Formula Learn Formula For Calculating A 3 B 3 Cuemath


A B 3 Formula Pdf
The expansion is (ab)³ = a³ 3a²b 3ab² b³ PROOF Lets draw a cube with side length (ab) , hence we know that the volume of this cube would be equal to (a b)3 Note that in the above diagram, the red part itself is a cube with volume a3 and the blue part is a cube with volume b3


Illustrations Of Formulas



Amazon Com Ab Solution Plus Vyotech Topical Ab Solution Fat Loss Formula 8oz 3 Pack Health Personal Care
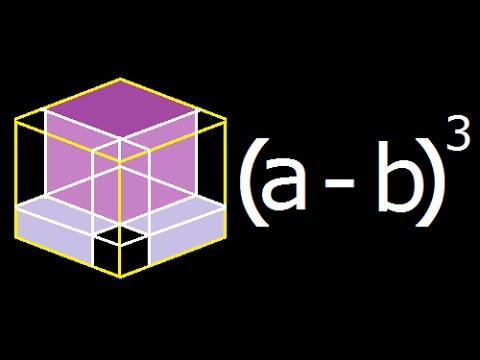


A Minus B Cube Or A Minus B Whole Cube A B 3 Geometric Explanation Derivation Youtube



Formula Of Ab 3 Is



23 The Chemical Formula For This Alloy System Can Be Expressed As Download Scientific Diagram



Jab 4 A B 14 The Simplest Formula Of A Com Pound Containing 50 Of Element A At Wt 10 And 50 Of Element B At Wt Is 1 Ab 2 Ab 3 Ab 4 A B


What Is The Formula Of Math A 3 B 3 Math Quora


How To Derive The Formula For A B 3 Without Using Numbers Quora
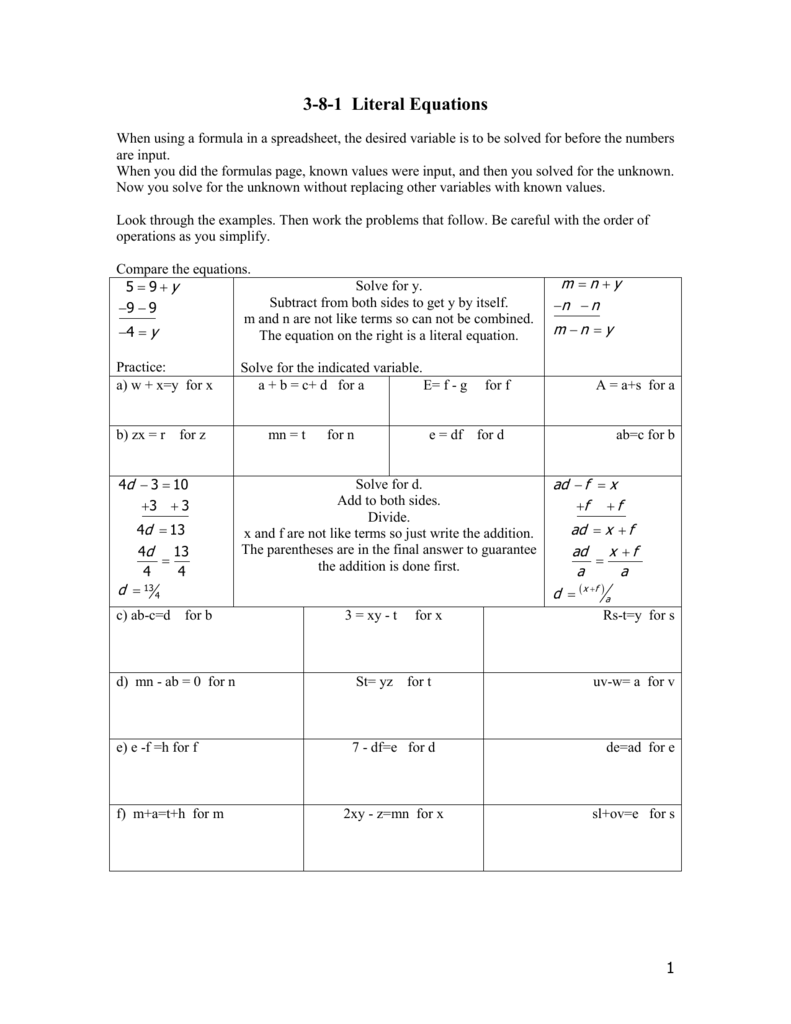


3 8 1 Literal Equations
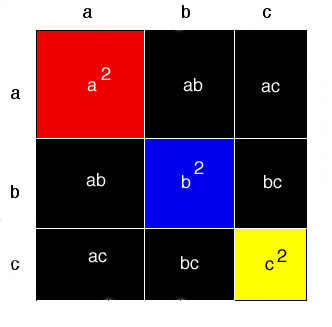


The Trinomial Cube


B2 Formula



Solved Es 11 Formula The Euclidean Distance Ab Between Chegg Com
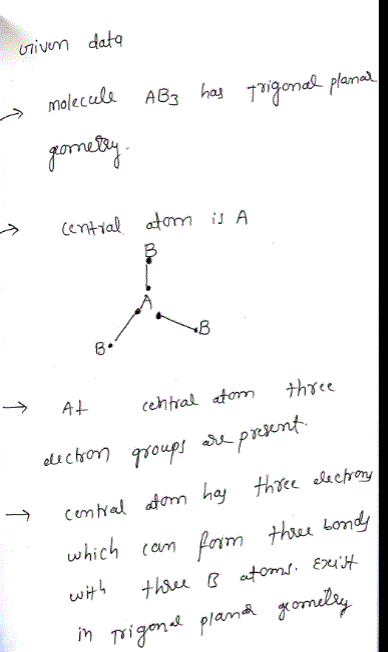


Oneclass A Molecule With The Formula Ab3 Has A Trigonal Planar Geometry How Many Electron Groups Ar


Www Jstor Org Stable
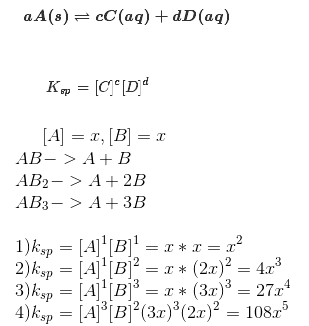


Express Ksp In Terms Of Molar Solubility X For A Salt With A Formula Of Ab S Ksp Ab2 S Ksp Ab3 S Home Work Help Learn Cbse Forum



Trigonometric And Geometric Conversions Sin A B Sin A B Sin Ab



13 Two Elements A And B Atomic Weights 75 And 16 Respectively Combine To Give A Compound Ha Ving 75 8 Of A The Compound Has The Formula St John S 1 Ab 2 Ab 3 Ab 4 A B



A B 2 Formula Learn Formula For Calculating A B 2 Cuemath



What Is A B 3 Quora



A B 7and A B 3 Then Find The Value Of A B 7 And A B 3 Then Find The Value Of Ab Brainly In
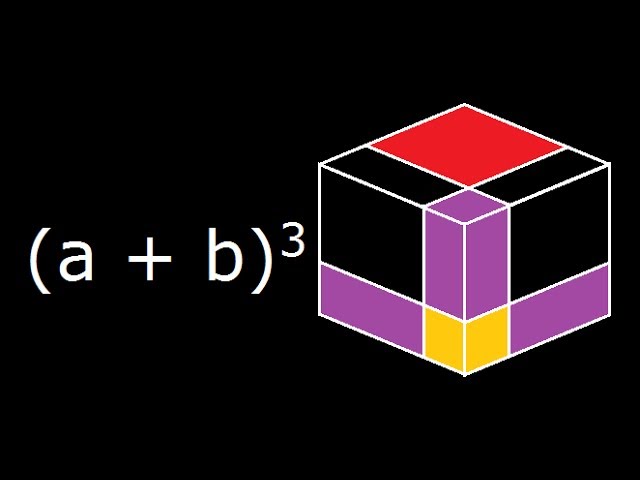


A B 3 A Plus B Cube Algebra Identity Geometrical Explanation And Derivation Youtube


Proof Of The Formula For A 3 B 3


What Is The Formula Of Math A 3 B 3 Math Quora



A B A B 3ab A B And A B A B 3ab A B Formula Proof By Easy Method Youtube


Search Q A3 2bb3 Formula Tbm Isch



What S The Formula Of A B Quora Learning Math Math Formula



A B 3 Expansion Formula



Factorise 250 A B 3 2 Mathematics Topperlearning Com 3dga2eee



00 28 Find The Area Of A Parallelogram Abcd In Which Ab 3 Cm And 4 Cm And Ac 5 Cm Using Heron S Formula Options A 6 Cm B 12 Cm C 18 Cm D 24 Cm


Solved Xor Gate Formula Select One 1 Ab Ab 2 A B Ab 3 Chegg Com


A B 3 Formula And Example Lunlun Com
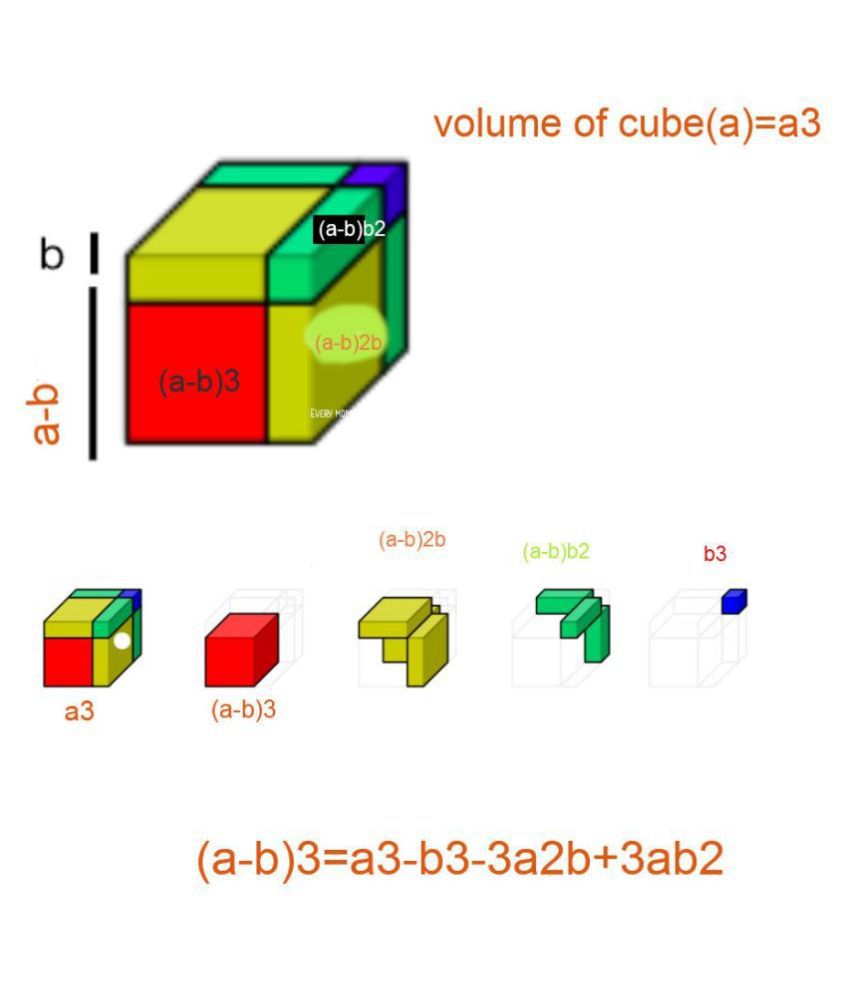


Mathworld Algebraic Identity Cube Set To Learn And Understand A B 3 Math Formula Manipulative Montessori Kids Learning Resources Kit Model For Maths Lab Buy Online At Best Price In India Snapdeal


Oneclass A Molecule With The Formula Ab3 Has A Trigonal Planar Geometry How Many Electron Groups Ar



A B Whole Cube Allexamhelp



What Is The Correct Formula Of Math A B 3 Math Quora



A B 3 Formula In Maths



Irrational Numbers Formula Algebra Formulas Teachoo Jpg Algebra Formulas Studying Math Learning Mathematics



Factorise A 3 B C 3 B 3 C A 3 C 3 A B 3


What Is The Formula Of Math A B 3 Math Quora



A B 3 I E A Plus B Cube Formula Proof Ntse Algebraic Formulas I Cube Proof Formula



Cube Formula Part 4 Siis A B 3 A3 3ab A B Youtube



Formula For A B Whole Cube Brainly In



Algebric Formula Mechanicalmilon


The Formula For A B 3 The Cube Of A Binomial Lunlun Com


What Is The Correct Formula Of Math A B 3 Math Quora



Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo



Using Quadratic Formula Solve For X 9x2 3 A B X Ab 0 Brainly In



What Is The Formula Of A B 3 2 Youtube



Find The Of 99 By Using Formula A B 3 Brainly In


What Is The Formula For Math A 3 B 3 Math Quora


Category Math Help Softmath Blog



ब जगण त स त र Docx


Mathematics Article Village Of Valparaiso Home School Inc



Square Of A Binomial A B 2 Math Formula Chart Formula Chart Math Formulas



Solved What Is The Simplest Formula Of The Compound Repre Chegg Com



Pdf Comparison Of Ab Formula And Soft Rotor Formula



In The Formula K A Ba B 2 Find The Value Of B If K 36 And A 3 Making B The Subject


Www Nextgurukul In Questions Answers Forum Question Academic Solve Using Quadratic Formula 9x2 3abxab 910



Tuesday July 1 Special Factoring Difference Of Squares Example M 2 64 M 2 8 2 M 8 M 8 Ppt Download



Prove That A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2
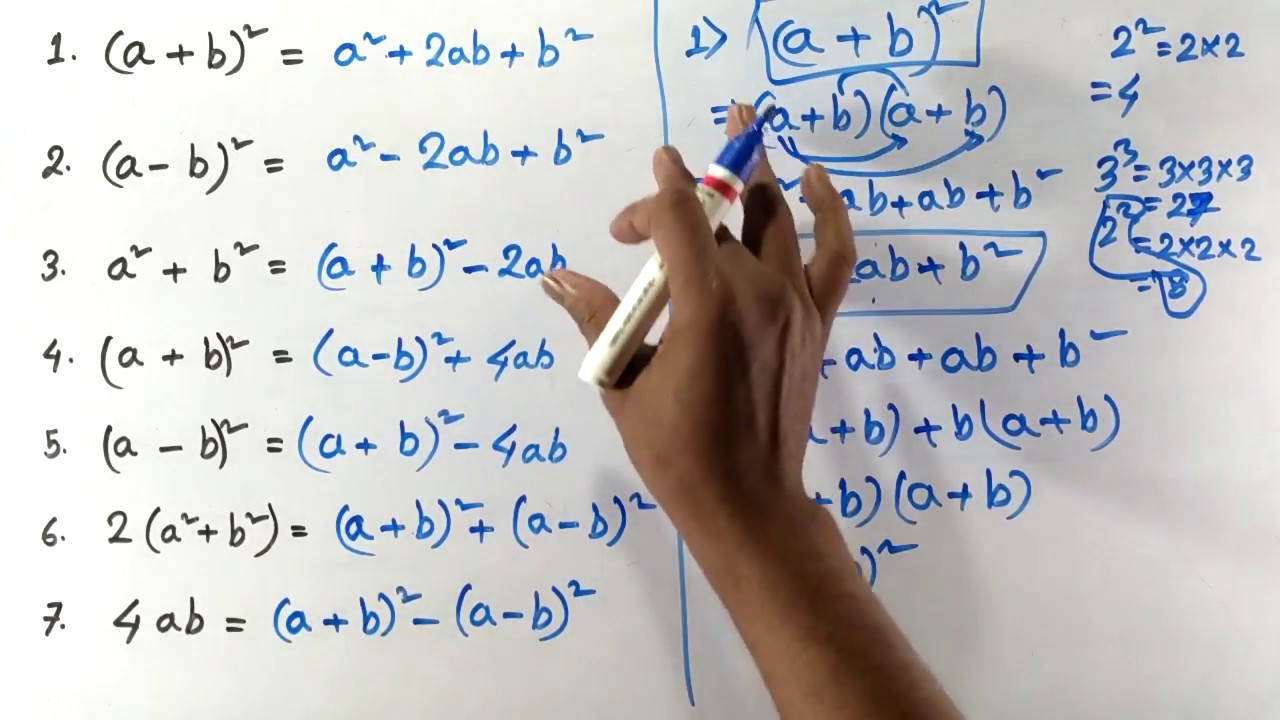


What Is Algebraic Formulas How To Remember Easily In Hindi Youtube


The Formula For A 3 B 3 The Difference Of Cubes Lunlun Com


Solved A Molecule With The Formula Ab 3 Has A Trigonal Planar Geometry How Many Electron Groups Are On The Central Atom Course Hero



What Is The Formula Of Math A B 3 Math Quora



All Formula With Example Of Algebric Expression Of Cube Brainly In


What Is The Correct Formula Of Math A B 3 Math Quora
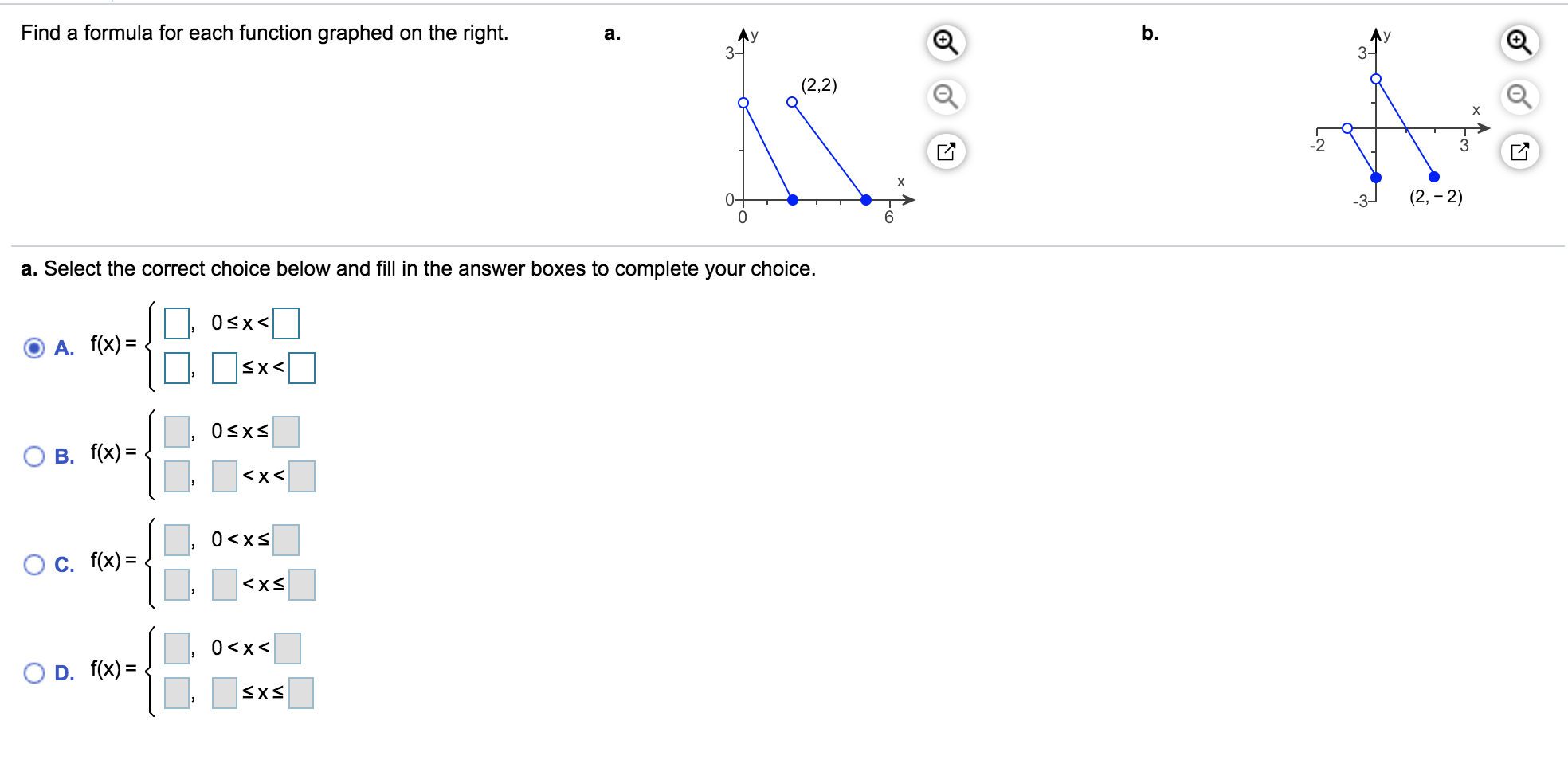


Solved Find A Formula For Each Function Graphed On The Ri Chegg Com
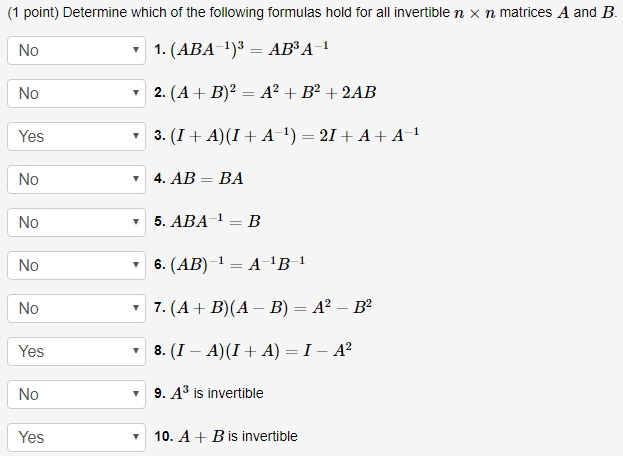


Solved Determine Which Of The Following Formulas Hold For Chegg Com



Yismxplusc Geometric Proof Of The Cubic Formula A B 3


Derivation Of Formula For A B 3
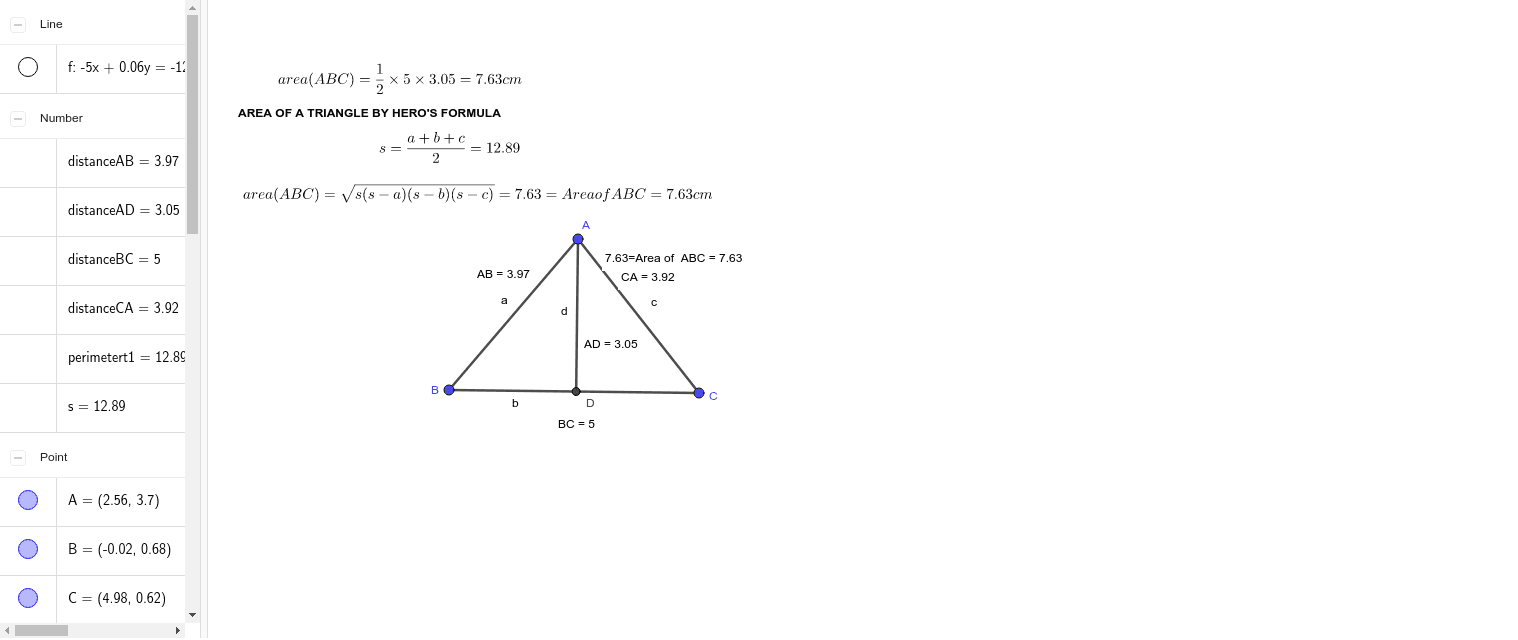


Hero S Formula Ch 12 Class Ix Geogebra
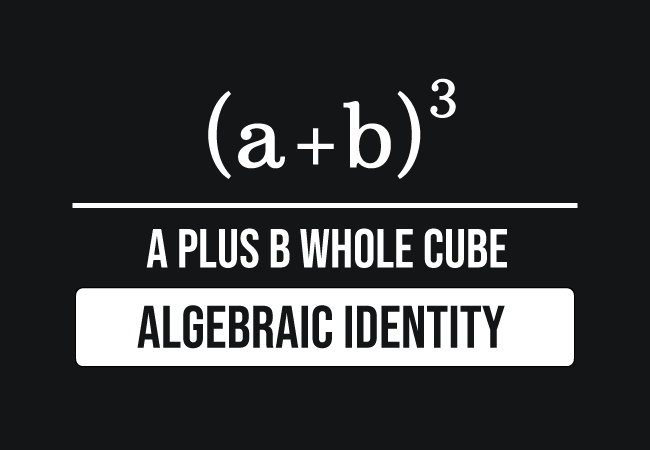


A B Formula Identity
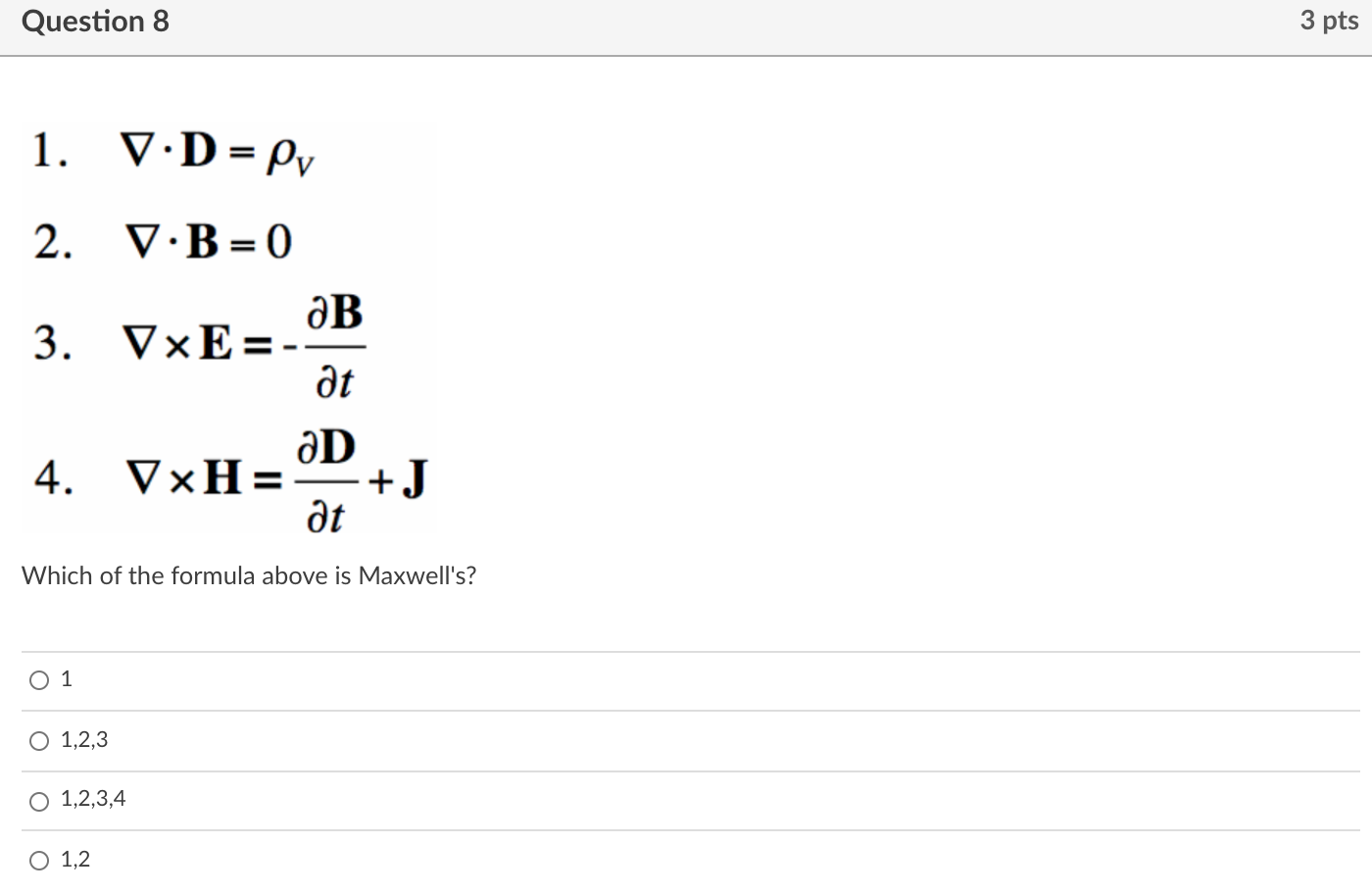


Solved Question 8 3 Pts 1 V D Pv 2 Vb 0 Ab 3 Vxe At Chegg Com



Formula Of Ab 3 Is Please Answer This Brainly In


コメント
コメントを投稿